回帰分析とは何か？メリット・デメリットと活用方法を解説
回帰分析の概要
回帰分析は、対象となるデータを説明や予測を行うための説明変数（もしくは予測変数）と、その基準となる目的変数に分けて、両者の間に統計モデルを設定し、その関係性を予測する手法です。目的変数yに説明変数xがどれだけの影響を与えるかを予測する方法となり、大きく分けて「単回帰分析」と「重回帰分析」の２種類に分けられます。
単回帰分析（single regression）
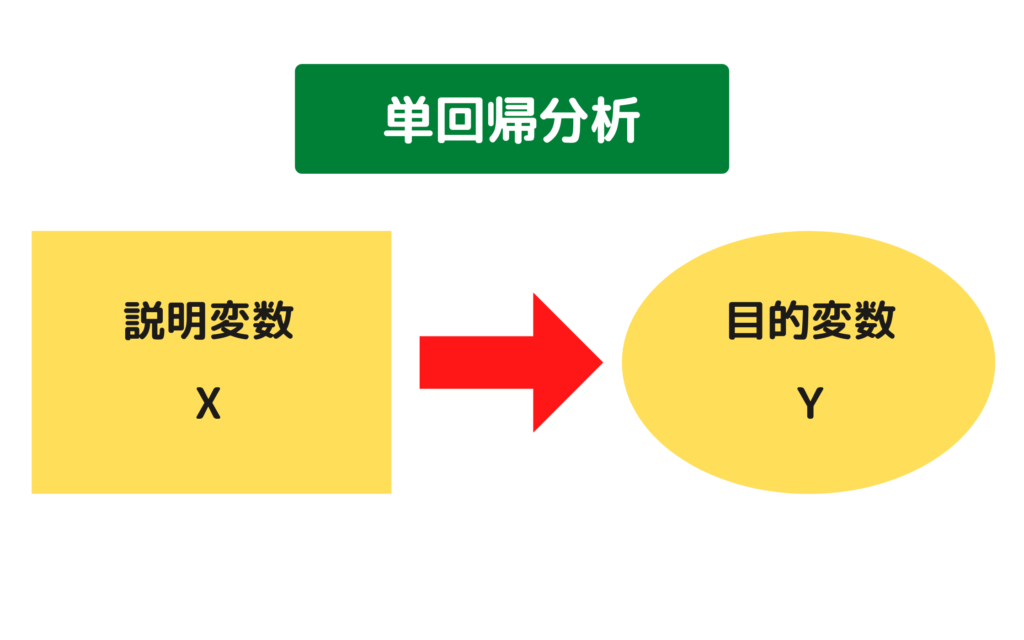
説明変数が１つであり、単一となる回帰分析を「単回帰分析」といいます。また説明変数が単一であることから「y＝ax+b」のグラフとなり、線形の関係を仮定して目的変数を予測することから「線形回帰分析」とも呼ばれます。
重回帰分析（multiple regression）
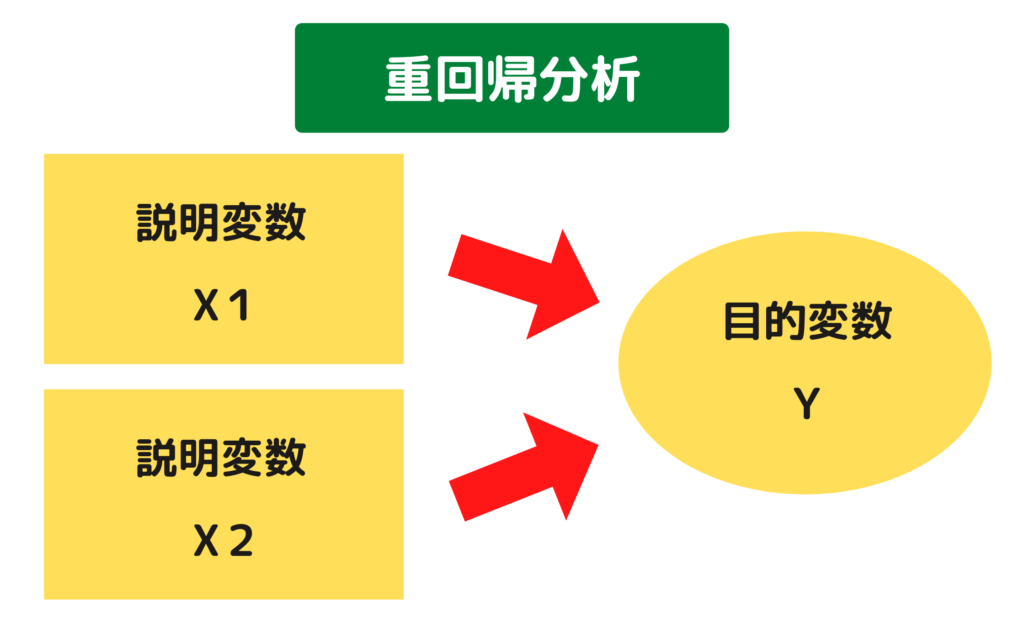
説明変数が２つ以上存在する線形回帰分析を「重回帰分析」といいます。重回帰分析は以下のような回帰式で示します。
- y = a1x1+a2x2+⋯+anxn+b
目的変数と予測変数の関係を線形以外で仮定する非線形回帰分析として「ロジスティック回帰分析」「多項式回帰分析」などもあります。
「相関関係」と「因果関係」の違い
回帰分析を理解する上で「相関関係」と「因果関係」への理解も必要となります。
相関関係は、一方の値が変化するともう一方の値も変化する関係のことであり、Xが増加するとき、Yも増加（または減少）します。２つの変数間に「原因⇒結果」の関係は必要なく、疑似相関の関係である可能性もあり注意が必要です。
一方、因果関係は、「原因⇒結果」の関係となり、原因が結果に直接影響を与えるものを示します。
回帰分析の難しいところは、目的変数と説明変数の関係が相関関係であるのか、因果関係であるのかは分析結果からは判断できないことです。
データ分析の際には因果関係の方が重要となりますが、回帰分析は関数をデータに当てはめることで、ある変数yの変動に対する別の変数xの変動からの影響関係を検討する手法となるため、回帰分析の結果は因果関係の証明にはなりえないことに注意する必要があります。
回帰分析のメリットとデメリット
回帰分析のメリットとデメリットとしては以下の通りです。
メリット
- 散布図に直線を当てはめて関係を予測するため視覚的に分かりやすい
- 数字を活用して統計データとして予測するため、根拠を示しやすい
- 数式に当てはめればデータがないところでも予測を行うことができる
デメリット
- 目的変数と説明変数を取り違えると誤った推論になる
回帰分析の活用例
インターネットサイトの閲覧データや集計したアンケート結果といったビッグデータから顧客の行動を予測することに活用できるため、マーケティングに活かすことができます。
回帰分析を用いてデータを正しく分析し、顧客やターゲット層、商品やサービスへの理解を深めることができます。