パレート図の概要
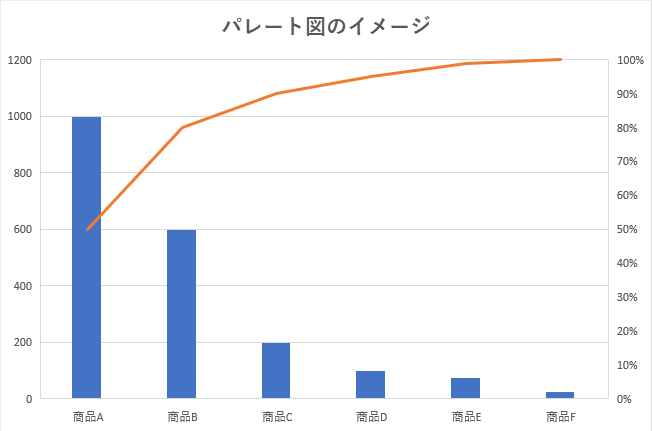
パレート図は、値が大きいものから順に(降順に)ソートされた棒グラフです。イタリアの経済学者ヴィルフレド・パレート(Vilfredo Frederico Damaso Pareto)に因んで名付けられました。
このパレート図は複数の項目の中で、どれが重要なのか、どの程度重要なのかを明示するために用いられます。
パレート図の用途
パレート図の用途を解説するために、ある企業の全商品の売上調査を考えます。
パレート図の横軸は品目、縦軸は各品目の売上です。売上が降順になるよう品目を並べてパレート図を描きます。パレート図を用いることで、どの商品が売上に多く貢献しているのか、他の商品の何倍の売上なのかが明確になります。
他にも、パレート図を使って不良品検査をする場合、横軸は品目、縦軸は各製品の不良率(不良品数/製造数)になります。ここでは、不良品が生じやすい製品が明確になります。
横軸は基本的に品目を取りますが、調査対象によって縦軸の値は都度変わります。
パレート図の描き方
パレート図は以下の手順で描くことができます。
- データの分類項目(売上や不良率など、パレート図の縦軸)を決め、集計する
- データの分類項目を降順に並び替える
- 分類項目が大きい順に棒グラフを描く
- 累積構成比を折れ線グラフで描く
累積構成比
パレート図には累積構成比を表す折れ線グラフを付すことが一般的です。
以下では商品の売上調査を例に累積構成比を解説します。
累積構成比を計算するにあたって、最も売上が多い品目を n=1番、2番目に多い品目を n=2番、、、売上が最も少ない品目をn=N番というようにすべての品目に番号を付けます。
Nは全品目数を意味しています。つまりN番目ということは最も売上の低い品目であることが分かります。
すると、m番目の品目の累積構成比は以下の式で計算することができます。
- 累積構成比 = 番号がm以下のすべての品目の売上の和 ÷すべての品目の売上の和
累積構成比は「m番目までの売上の和が全体に占める割合」を表しており、n=N番の品目においては累積構成比は必ず1になります。
パレートの法則とABC分析
パレートの法則
経済学において「全体の数値の大部分は、全体の中の一部の要素が生み出している」という経験則をパレートの法則と呼びます。
例えば、企業の売上に注目すると、売上の8割が全商品銘柄のうち2割の商品で生み出されている場合、その企業の売上はパレートの法則に従っています。
あるいは、売上の8割を生み出しているのが、全顧客中の2割の顧客である場合も、パレートの法則に従った売上になっています。
ABC分析(重点分析)とは
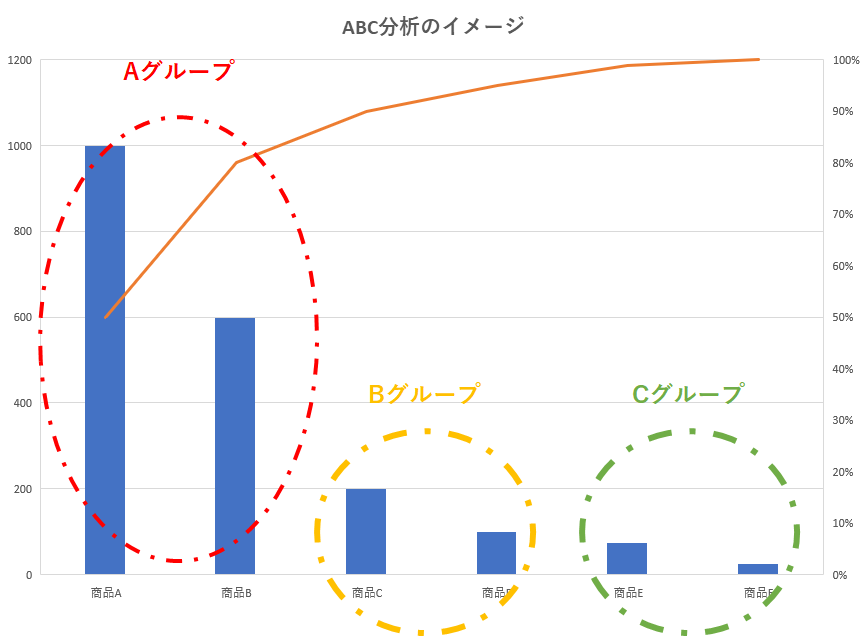
ABC分析とはパレート図中の品目を重要度別にA、B、Cの3グループに分ける手法で、売上調査や販売計画、品質管理、在庫管理などに用いられます。
売上調査であれば、「グループ分け基準」や「グループ分けをした後の管理体制」は以下のようになります。
- A → 累積構成比 0~0.8 の品目。在庫管理では十分な保管場所を確保し、品切れを防ぐべく事前に発注を行う。回転が速いので多めに納品しても余剰在庫となりにくい。
- B → 累積構成比 0.8~0.9 の品目。在庫切れを見計らって発注を行う。
- C → 累積構成比 0.9~1 の品目。在庫切れによる機会損失も止む無し。納品頻度を下げる。
これらのグループの分け方には明確な決まりがあるわけではなく、ABCの3グループに分けるのが一般的ですが、用途や目的によってはグループ数が4つや5つになる場合もあります。
ABC分析のメリット
ABC分析のメリットは「資源の適切な分配」ができることです。
パレートの法則が示す通り、売上の大部分が2割の商品で生み出されるならば、その2割の商品を他の商品と区別し、重点的に管理する方が効率的です。
そのため、ABC分析を行い、その2割の商品を識別していきます。
このパレートの法則を利用して売上を伸ばしている例として、駅に出店している本屋が挙げられます。
駅の本屋はスペースの制約から、商品の種類を増やすことは容易ではありません。そのため、売れている本の上位2割だけを仕入れて、本の種類が少なくとも売上が上がるようにしています。